Pitagorasz tétele:
A derékszögű háromszög befogóira rajzolt négyzetek területeinek összege egyenlő az átfogóra rajzolt négyzet területével.
A derékszögű háromszög befogóira rajzolt négyzetek területeinek összege egyenlő az átfogóra rajzolt négyzet területével.
Algebrai alakban: 
, ahol a és b a derékszögű háromszög két befogója és c az átfogója.
, ahol a és b a derékszögű háromszög két befogója és c az átfogója.
Bizonyítás:
I. A legismertebb
Az ábráról leolvasható a tétel bizonyítása.
A két 
oldalú négyzet területe egyenlő, és ha mindkettőből elvesszük az eredeti háromszög területének 4-szeresét, akkor egyenlő területeket kapunk.
oldalú négyzet területe egyenlő, és ha mindkettőből elvesszük az eredeti háromszög területének 4-szeresét, akkor egyenlő területeket kapunk.
II. A befogó-tétel segítségével
Legyen a háromszög két befogója a és b az átfogója pedig c! Ossza az átfogót a hozzá tartozó magasság
és 
részre!
és részre!
Ekkor a befogó tételt felírva:
A két egyenletet összeadva:
A Pitagorasz-tétel megfordítása:
Ha egy háromszög két oldalának négyzetösszege egyenlő a harmadik oldal négyzetével, akkor a háromszög derékszögű.
Vegyünk egy háromszöget, melyre teljesül, hogy 
, ahol a, b és c a háromszög oldalai!
Be fogjuk látni, hogy derékszögű.
Az a és b befogójú derékszögű háromszög átfogója legyen
! Írjuk fel a Pitagorasz-tételt erre a háromszögre!
A két egyenletet összevetve kapjuk, hogy
, amiből 
következik. Ez viszont azt jelenti, hogy a két háromszög oldalai megegyeznek, így a két háromszög egybevágó, ezért az eredeti háromszögnek is van derékszöge.
, ahol a, b és c a háromszög oldalai!Be fogjuk látni, hogy derékszögű.
Az a és b befogójú derékszögű háromszög átfogója legyen
! Írjuk fel a Pitagorasz-tételt erre a háromszögre!A két egyenletet összevetve kapjuk, hogy
, amiből következik. Ez viszont azt jelenti, hogy a két háromszög oldalai megegyeznek, így a két háromszög egybevágó, ezért az eredeti háromszögnek is van derékszöge.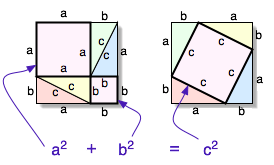
0 megjegyzés:
Megjegyzés küldése